Bloch Vector Explained: Visualizing Qubit States
2025.03.24 · Blog
Introduction: What Is a Bloch Vector?
In quantum computing, the Bloch vector provides an intuitive geometric representation of a single qubit's state. Instead of thinking in terms of complex wavefunctions, quantum states can be visualized as a point on or inside the Bloch sphere, with the Bloch vector pointing from the center of the sphere to that point.
This visualization is crucial for understanding how qubits evolve, how quantum gates operate, and how measurements work in quantum algorithms.
Mathematical Definition of Bloch Vector
A single qubit state is generally expressed as:
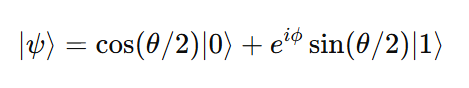
Here:
-
θ (theta): The polar angle from the z-axis (0 ≤ θ ≤ π)
-
φ (phi): The azimuthal angle around the z-axis (0 ≤ φ < 2π)
The Bloch vector r has components:
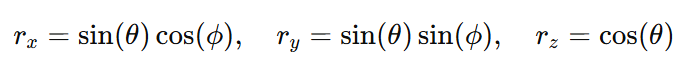
This vector r = (r_x, r_y, r_z) points from the center of the Bloch sphere to the qubit's state.
Bloch Sphere and Its Interpretation
The Bloch sphere is a 3D unit sphere where:
-
|0⟩ state is at the North Pole (r_z = +1)
-
|1⟩ state is at the South Pole (r_z = -1)
-
Equal superposition states (like |+⟩ and |−⟩) lie on the equator
Any arbitrary qubit state can be represented as a unique point on this sphere. The Bloch vector's length is typically 1 for pure states and less than 1 for mixed states.
Quantum Gates as Rotations of the Bloch Vector
One of the most powerful aspects of the Bloch vector is that quantum gates can be visualized as rotations of the vector:
-
X gate: 180-degree rotation around the X-axis
-
Y gate: 180-degree rotation around the Y-axis
-
Z gate: Rotation around the Z-axis
-
Hadamard gate: Rotation that brings the vector from the pole to the equator
By visualizing these transformations, quantum computing becomes far more intuitive.
Bloch Vector and Quantum Measurement
The measurement probability is related to the Bloch vector's position.
Measuring in the computational basis:
- Probability of |0⟩ = (1 + r_z) / 2
- Probability of |1⟩ = (1 - r_z) / 2
This relationship shows why the Bloch vector is essential for understanding qubit outcomes.
Why the Bloch Vector Matters
-
Intuitive visualization: It shows how quantum states evolve.
-
Gate operations: Quantum gates are rotations of the Bloch vector.
-
Measurement: The direction of the vector indicates the probability outcomes.
Practical Applications of the Bloch Vector
-
Quantum education: Teaching quantum mechanics and algorithms visually
-
Quantum debugging: Visualizing qubit states during quantum circuit execution
-
Quantum state tomography: Reconstructing qubit states in experiments
-
Quantum hardware calibration: Understanding errors and noise by analyzing state vectors
Examples of Common Bloch Vector States
| State | Bloch Vector (r_x, r_y, r_z) | Position on Bloch Sphere |
| |0⟩ | (0, 0, +1) | North Pole |
| |1⟩ | (0, 0, -1) | South Pole |
| |+⟩ = ( | 0⟩+ | 1⟩)/√2 |
| |−⟩ = ( | 0⟩− | 1⟩)/√2 |
| |i⟩ = ( | 0⟩ + i | 1⟩)/√2 |
Conclusion
The Bloch vector is a powerful concept that makes the complex world of qubit states much more accessible. Whether you're learning quantum computing, visualizing quantum gates, or working with quantum hardware, understanding the Bloch vector and Bloch sphere will help you interpret and design quantum operations with confidence.
Featured Content
Popular Reads




.png)

