Master Quantum Fidelity: What It Means and Why It Matters

Quantum computing relies on delicate quantum states to perform computations. However, these states are highly susceptible to errors due to decoherence and external noise. Quantum fidelity is a fundamental metric that quantifies the accuracy and stability of quantum states, making it a critical tool for assessing quantum operations, error correction protocols, and overall system reliability.

But what exactly is quantum fidelity, and why does it matter in quantum systems?

In this article, we'll break down:

•  What quantum fidelity is and how it's calculated

• Why quantum fidelity matters in quantum computation, and its role in improving quantum algorithms and error correction

• How improving quantum fidelity enhances real-world quantum computing applications

Let's dive in!

What is Quantum Fidelity?

Quantum fidelity is a measure of how closely an actual quantum state or quantum process matches its ideal or expected state. In other words, it tells us how “faithfully” a quantum system behaves when compared to a target or desired outcome.

Mathematically, quantum fidelity is defined as the overlap between two quantum states. If two states are identical, the fidelity is 1. If they are completely different, the fidelity is 0.

High fidelity indicates a well-preserved quantum state, whereas low fidelity suggests significant deviations caused by noise, imperfect quantum gates, or decoherence effects.

This measure is particularly important in quantum mechanics, where small errors or deviations can significantly affect the outcome of quantum algorithms and computations.

How is Quantum Fidelity Calculated?

Mathematically, the fidelity F between two quantum states, represented by density matrices ρ and σ, is defined as:

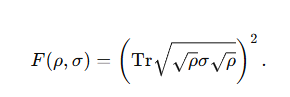
For pure states∣ψ⟩ and ∣ϕ⟩, the fidelity simplifies to:

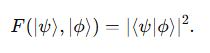
This formula quantifies the overlap between two quantum states, with F=1 indicating perfect similarity. This value ranges from 0 (completely different states) to 1 (identical states), providing a clear measure of state preservation in quantum computations.

The closer the fidelity is to 1, the better the system's performance. A high fidelity indicates that the quantum state or operation has been executed with minimal error, while a low fidelity signals that errors have affected the system's behavior.

In real-world applications, quantum fidelity is often used to evaluate the effectiveness of quantum gates, quantum circuits, and quantum algorithms. Researchers strive to push fidelity closer to 1, making quantum computers more practical and reliable for solving complex problems.

Why is Quantum Fidelity Important?

#1 Enhancing Quantum Error Correction

One of the primary uses of quantum fidelity is in quantum error correction. Quantum systems are inherently fragile, and maintaining the fidelity of quantum states is a major challenge. Small interactions with the environment can lead to errors, known as quantum decoherence, which degrade the performance of quantum computers. Monitoring fidelity allows researchers to detect and correct these errors, ensuring that quantum computations remain accurate and reliable.

#2 Ensuring Accuracy in Quantum Algorithms and Computational Performance

High fidelity in quantum computations means better accuracy in quantum algorithms. For algorithms like Shor's algorithm or Grover's algorithm, which are designed to solve specific problems faster than classical computers, maintaining high fidelity is critical. If the fidelity of the quantum state drops, the algorithm may produce incorrect or unreliable results, undermining the potential benefits of quantum computing.

#3 Optimizing Quantum Systems

Fidelity is also a useful tool for optimizing quantum systems. In experiments and real-world quantum applications, researchers continually work to improve the fidelity of quantum gates and quantum circuits. Higher fidelity means that quantum operations are performed with greater precision, which ultimately leads to more reliable and efficient quantum computers.

#4 Ensuring Secure Quantum Communication with High Fidelity

Fidelity is vital in quantum networks and quantum key distribution (QKD) to guarantee secure transmission of quantum information.

How to Enhance Quantum Fidelity in Quantum Systems

To improve fidelity and reduce errors in quantum systems, several strategies are employed:

Quantum Error Correction (QEC)

Quantum Error Correction (QEC) involves encoding quantum information across multiple qubits to protect it from noise. Key error-correcting codes include:

Surface Codes: These are widely used for fault-tolerant quantum computing and spread quantum information over a 2D array, ensuring reliable operations even with errors.

Shor's Code and Steane Code: These codes use redundancy to encode quantum information, helping to recover it from noise and errors, improving overall fidelity.

Noise Mitigation Techniques

Noise mitigation techniques help reduce the impact of errors and improve the performance of near-term quantum processors, also known as Noisy Intermediate-Scale Quantum (NISQ) devices.

Zero-Noise Extrapolation: This method runs quantum algorithms at varying noise levels and extrapolates the results to estimate the ideal outcome without noise, enhancing accuracy in near-term quantum processors.

Error Suppression: Techniques like Dynamical Decoupling help reduce decoherence by applying control pulses to cancel environmental interactions, boosting fidelity.

Quantum Gate Calibration: Regular calibration of quantum gates ensures that operations remain accurate, thus maintaining high fidelity throughout the quantum algorithm.

Quantum Hardware Improvements

Advances in hardware design and manufacturing techniques directly contribute to reducing noise and decoherence, ultimately enhancing quantum state preservation.

Qubit Design: Superconducting qubits, trapped ions, and photon-based qubits are improved to reduce noise and increase coherence times, enhancing fidelity.

Cryogenic Cooling: Operating quantum systems at ultra-low temperatures reduces thermal noise, helping preserve quantum states and improve fidelity.

High-Fidelity Quantum Gates: As quantum computers scale up, high-fidelity quantum gates become increasingly important. Advanced gate design techniques, such as cross-resonance gates and optimal pulse shaping, enable more accurate control over qubits during quantum operations. These gates help reduce errors that would otherwise impact fidelity.

Optimal Control Methods

Optimal control theory is applied to quantum systems to design quantum gates that minimize errors. By carefully controlling the quantum system's evolution through external driving fields, researchers can design pulses that drive qubits along specific paths, avoiding unintended interactions.

Pulse Shaping: Optimizing control pulses minimizes errors during gate operations, improving fidelity.

Adaptive Quantum Control: Real-time adjustment of control parameters compensates for system drifts, ensuring high fidelity throughout the computation.

Improving fidelity is not just about reducing errors but ensuring that quantum computers can operate effectively in the presence of noise, bringing us closer to realizing practical quantum technologies for real-world applications.

Conclusion

In summary, quantum fidelity is a cornerstone of quantum computing. It measures how accurately a quantum system behaves and ensures that quantum algorithms and operations are performed with the highest precision.

Whether it's quantum error correction, optimizing quantum systems, or improving algorithm performance, understanding and improving quantum fidelity is crucial for the success of quantum computing.

As the field of quantum computing progresses, we can expect quantum fidelity to remain a key area of focus, helping researchers build more powerful, reliable, and scalable quantum computers.