Ultimate Guide to Quantum Gates: Everything You Need to Know

Quantum computing represents a transformative leap in how we process information, promising unprecedented computational power that classical computers cannot match. At the heart of this revolutionary technology are quantum gates, the fundamental building blocks that control and manipulate quantum bits (qubits).

In this article, we will explore what quantum gates are, their various types, how they work, and their pivotal role in quantum algorithms and applications.

What Are Quantum Gates?

In classical computing, logic gates like AND, OR, and NOT are used to perform operations on bits, the basic units of information. Similarly, quantum gates are the operations that manipulate qubits, the fundamental unit of information in quantum computing.

While classical logic gates are deterministic, quantum gates operate probabilistically, taking advantage of quantum phenomena like superposition and entanglement. This allows quantum gates to process information in ways that classical gates cannot, enabling quantum computers to perform complex calculations that would be practically impossible for classical systems.

Key Characteristics of Quantum Gates

Non-Deterministic: Quantum gates can create a superposition of different states, giving quantum computers their unique power.

Unitary Operations: Quantum gates are represented by unitary matrices, meaning they preserve the total probability of all possible outcomes (i.e., no information is lost during their operation).

Types of Quantum Gates

There are various types of quantum gates, each serving different functions in quantum computations. These gates are classified into single-qubit gates and multi-qubit gates, based on how many qubits they act upon.

1. Basic Quantum Gates

X Gate (Pauli-X Gate): This gate acts as a quantum version of the classical NOT gate. It flips the state of a qubit. If the qubit is in state ∣0⟩, it flips to ∣1⟩, and vice versa. The matrix representation of the X gate is:

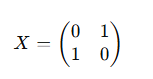
Z Gate (Pauli-Z Gate): The Z gate applies a phase flip to the qubit without changing its state. It introduces a phase of Π to the qubit's amplitude in the ∣1⟩ state, while leaving ∣0⟩ unchanged:

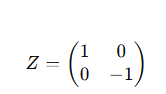
Y Gate (Pauli-Y Gate): A combination of the X and Z gates, the Y gate introduces a phase shift and flips the qubit state. Its matrix representation is:

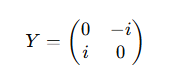
2. Rotation Gates

Rotation gates (Rx, Ry, Rz) are used to rotate a qubit around a specific axis (X, Y, or Z). These gates provide more precise control over a qubit's state, which is critical in quantum algorithms.

Rx, Ry, Rz Gates: These gates rotate the qubit's state around the X, Y, or Z axis by a given angle. They are represented by:

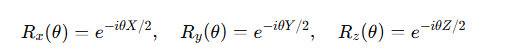
3. Hadamard Gate (H Gate)

The Hadamard gate is one of the most important quantum gates. It creates superposition, a state where a qubit exists in both ∣0⟩ and ∣1⟩ simultaneously, with equal probability. This is essential for quantum parallelism. The matrix representation is:

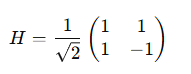
4. CNOT Gate (Controlled-NOT Gate)

The CNOT gate is a two-qubit gate that flips the state of the second qubit (the target) if the first qubit (the control) is in the ∣1⟩ state. This gate is widely used for creating entanglement between qubits, which is a key feature of quantum computing. Its matrix representation is:

5. Toffoli Gate (CCNOT Gate)

The Toffoli gate is a three-qubit gate that performs a NOT operation on the third qubit (the target) only if the first two qubits (the controls) are both in the ∣1⟩ state. This gate is an important part of many quantum error-correcting codes and quantum simulations.

6. SWAP Gate

The SWAP gate exchanges the states of two qubits. It is used to rearrange the qubits in quantum algorithms. The matrix for a SWAP gate is:

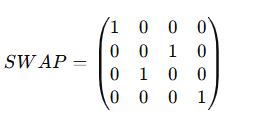
How Do Quantum Gates Work?

Quantum gates operate on qubits and change their states. The state of a qubit is represented by a complex vector in a two-dimensional space (using Dirac notation). A quantum gate is essentially a matrix that acts on this vector, transforming it into another vector.

For example, the Hadamard gate transforms a qubit in the state ∣0⟩ into a superposition:

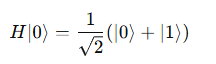
Quantum gates work by manipulating these superpositions and entanglements, allowing quantum computers to perform parallel operations on many possible solutions simultaneously, unlike classical computers which process one solution at a time.

Applications of Quantum Gates in Quantum Computing

Quantum gates form the foundation of quantum algorithms, enabling quantum computers to solve problems that are intractable for classical computers. Let's explore their role in some key areas:

1. Quantum Algorithms

Quantum algorithms like Shor's algorithm (for factoring large numbers) and Grover's search algorithm (for searching unsorted databases) rely heavily on the use of quantum gates to perform operations in superposition. These algorithms can offer exponential speedups over classical counterparts.

2. Quantum Error Correction

Since quantum gates are highly sensitive to errors due to decoherence and noise, quantum error correction is a crucial component of large-scale quantum computers. Quantum gates are used in error correction codes (e.g., the surface code) to detect and correct errors that may occur during computation, ensuring the integrity of quantum information.

3. Quantum Computers

Different quantum computing platforms, such as superconducting qubits, trapped-ion qubits, and topological qubits, utilize quantum gates to manipulate qubits. These gates are executed by precise control pulses that influence the quantum state of the system, enabling complex computations.

Challenges and Future of Quantum Gates

Despite their promise, quantum gates face significant challenges:

Precision and Noise: Quantum gates require extremely high precision, and noise is a major challenge. Small errors in gate operations can propagate and affect the outcome of calculations.

Scalability: Implementing large numbers of quantum gates to solve practical problems requires overcoming challenges related to error correction, hardware noise, and qubit connectivity.

However, advancements in quantum hardware, error correction, and gate fidelity are steadily improving. In the future, we expect to see more reliable and efficient quantum gates that will unlock the full potential of quantum computing.

Conclusion

Quantum gates are the backbone of quantum computing, enabling quantum computers to perform tasks that classical computers cannot. With a range of gate types that manipulate qubits in various ways, quantum gates empower algorithms, quantum error correction, and complex computations.

As quantum hardware improves, the precision and scalability of quantum gates will play a crucial role in advancing quantum computing and opening new doors to solving real-world problems.